Gyroskop-Regelung im Roboter

Erklärung der Gyroskop-Regelung im Roboter

1. Ziel der Regelung

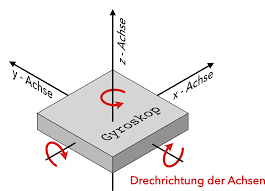
Das Gyroskop misst kontinuierlich die Drehgeschwindigkeit um die Z-Achse des Roboters. Unser Ziel ist es, den Roboter auf einem gewünschten Winkel (z. B. geradeaus) zu halten, auch wenn äußere Kräfte (z. B. Bodenunebenheiten) versuchen, ihn davon abzubringen.

2. Sensorik

Das Gyroskop (LSM6DS3) liefert Winkelgeschwindigkeiten in Grad/Sekunde. Durch Integration dieser Geschwindigkeit über die Zeit angle += gyro_z * dt erhält man den aktuellen Kurswinkel.

images1.jpg image2.jpg image3.png

 

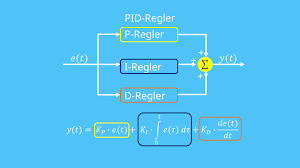
3. PID-Regelung

Der Roboter verwendet eine PID-Regelung (Proportional-Integral-Derivative), um die Abweichung vom Sollwinkel zu korrigieren:

  • P-Anteil: reagiert direkt auf den Fehler (Ist - Soll)
  • I-Anteil: summiert Fehler über die Zeit (gegen dauerhafte Abweichung)
  • D-Anteil: berücksichtigt die Änderungsrate des Fehlers (für Dämpfung)

Die Korrektur wird wie folgt berechnet:
correction = Kp * error + Ki * integral + Kd * derivative

image4.png

 

4. Motorsteuerung

Die berechnete correction wird direkt auf die linke und rechte Motorleistung angewendet:

left  = speed + correction
right = speed - correction

So wird der Roboter aktiv auf Kurs gehalten: weicht er ab, kompensieren die Motoren die Differenz. Das erfolgt 100-mal pro Sekunde (10 ms Takt).

5. Ergebnis

Der Roboter kann über eine Strecke konstant geradeaus fahren – auch wenn das Gelände leicht schief ist oder einseitiger Widerstand besteht. Die Kursregelung erfolgt in Echtzeit im Millisekundentakt.

Der PID-Regler reagiert flexibel auf Abweichungen, sorgt für ruhigen Lauf und stoppt automatisch, wenn ein Hindernis erkannt wird (per Echo-Sensor).

6. Erweiterungsidee

Künftig kann der Roboter auch in Kurven fahren, indem der target_angle während der Fahrt dynamisch angepasst wird. Auch ein zweiter Sensor für Seitenabweichungen wäre denkbar.